12 Named Discrete Distributions
12.1 Objectives
Recognize and set up for use common discrete distributions (Uniform, Binomial, Poisson, Hypergeometric) to include parameters, assumptions, and moments.
Use
Rto calculate probabilities and quantiles involving random variables with common discrete distributions.
12.2 Homework
For each of the problems below, 1) define a random variable that will help you answer the question, 2) state the distribution and parameters of that random variable; 3) determine the expected value and variance of that random variable, and 4) use that random variable to answer the question.
We will demonstrate using 1a and 1b.
12.2.1 Problem 1
The T-6 training aircraft is used during UPT. Suppose that on each training sortie, aircraft return with a maintenance-related failure at a rate of 1 per 100 sorties.
- Find the probability of no maintenance failures in 15 sorties.
\(X\): the number of maintenance failures in 15 sorties.
\(X\sim \textsf{Bin}(n=15,p=0.01)\)
\(\mbox{E}(X)=15*0.01=0.15\) and \(\mbox{Var}(X)=15*0.01*0.99=0.1485\).
\(\mbox{P}(\mbox{No maintenance failures})=\mbox{P}(X=0)={15\choose 0}0.01^0(1-0.01)^{15}=0.99^{15}\)
0.99^15## [1] 0.8600584
## or
dbinom(0,15,0.01)## [1] 0.8600584This probability makes sense, since the expected value is fairly low. Because, on average, only 0.15 failures would occur every 15 trials, 0 failures would be a very common result. Graphically, the pmf looks like this:
gf_dist("binom",size=15,prob=0.01) %>%
gf_theme(theme_classic())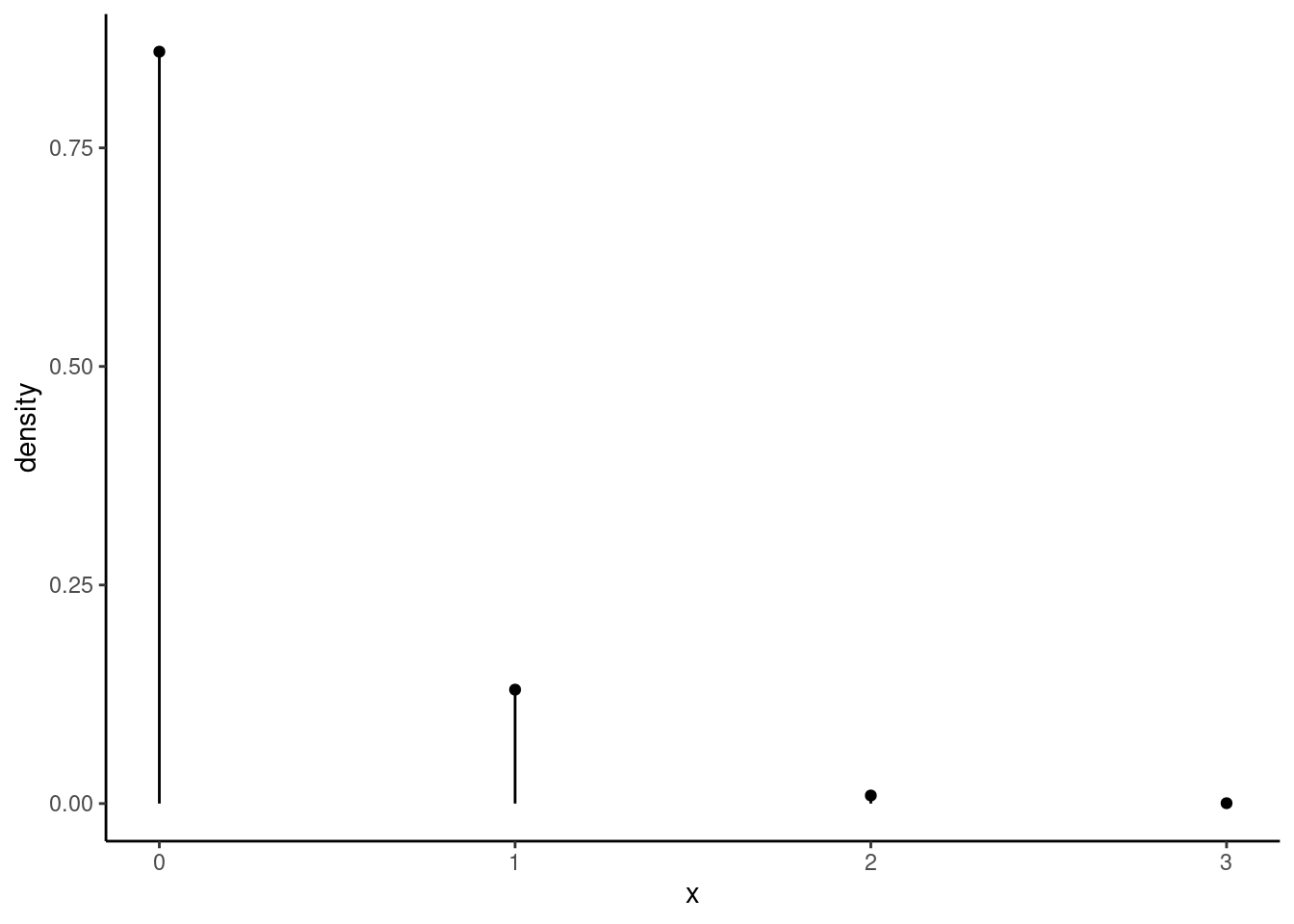
- Find the probability of at least two maintenance failures in 15 sorties.
We can use the same \(X\) as above. Now, we are looking for \(\mbox{P}(X\geq 2)\). This is equivalent to finding \(1-\mbox{P}(X\leq 1)\):
## Directly
1-(0.99^15 + 15*0.01*0.99^14)## [1] 0.009629773## [1] 0.009629773## [1] 0.009629773
## or
1-pbinom(1,15,0.01)## [1] 0.009629773
## or
pbinom(1,15,0.01,lower.tail = F)## [1] 0.009629773- Find the probability of at least 30 successful (no mx failures) sorties before the first failure.
\(X\): the number of maintenance failures out of 30 sorties.
\(X\sim \textsf{Binom}(n=30,p=0.01)\), and \(\mbox{E}(X)=0.3\) and \(\mbox{Var}(X)=0.297\).
\(\mbox{P}(\mbox{0 failures})=\mbox{P}(X=0)=0.99^{30}\)
0.99^30## [1] 0.7397004
##or
dbinom(0,30,0.01)## [1] 0.7397004Using negative binomial, which was not in the reading but you can research:
\(Y\): the number of successful sorties before the first failure.
\(Y\sim \textsf{NegBin}(n=1,p=0.01)\), and \(\mbox{E}(X)=99\) and \(\mbox{Var}(X)=9900\).
\(\mbox{P}(\mbox{at least 30 successes before first failure})=\mbox{P}(Y\geq 30)\)
1-pnbinom(29,1,0.01)## [1] 0.7397004- Find the probability of at least 50 successful sorties before the third failure.
Using a binomial random variable, we have 52 trials and need at least 50 to be a success. The random variable is \(X\) the number of successful sorties out of 52.
1-pbinom(49,52,.99)## [1] 0.9846474Or using a negative binomial, let
\(Y\): the number of successful sorties before the third failure.
\(Y\sim \textsf{NegBin}(n=3,p=0.01)\), and \(\mbox{E}(X)=297\) and \(\mbox{Var}(X)=29700\).
\(\mbox{P}(\mbox{at least 50 successes before 3rd failure})=\mbox{P}(Y\geq 50)\)
1-pnbinom(49,3,0.01)## [1] 0.9846474Notice if the question had been exactly 50 successful sorties before the 3 failure, that is a different question. Then we could use either:
dbinom(50,52,.99)*.01## [1] 0.000802238The \(0.01\) is because the last trial is a failure.
Or
dnbinom(50,3,0.01)## [1] 0.00080223812.2.2 Problem 2
On a given Saturday, suppose vehicles arrive at the USAFA North Gate according to a Poisson process at a rate of 40 arrivals per hour.
- Find the probability no vehicles arrive in 10 minutes.
\(X\): number of vehicles that arrive in 10 minutes
\(X\sim \textsf{Pois}(\lambda=40/6=6.67)\) and \(\mbox{E}(X)=\mbox{Var}(X)=6.67\).
\(\mbox{P}(\mbox{no arrivals in 10 minutes})=\mbox{P}(X=0)=\frac{6.67^0 e^{-6.67}}{0!}=e^{-6.67}\)
exp(-40/6)## [1] 0.001272634
##or
dpois(0,40/6)## [1] 0.001272634- Find the probability at least 50 vehicles arrive in an hour.
\(X\): number of vehicles that arrive in an hour
\(X\sim \textsf{Pois}(\lambda=40)\) and \(\mbox{E}(X)=\mbox{Var}(X)=40\).
\(\mbox{P}(\mbox{at least 50 arrivals in 1 hour})=\mbox{P}(X\geq 50)\)
1-ppois(49,40)## [1] 0.07033507- Find the probability that at least 5 minutes will pass before the next arrival.
\(X\): number of vehicles that arrive in 5 minutes
\(X\sim \textsf{Pois}(\lambda=40/12=3.33)\) and \(\mbox{E}(X)=\mbox{Var}(X)=3.33\).
\(\mbox{P}(\mbox{no arrivals in 5 minutes})=\mbox{P}(X=0)=\frac{3.33^0 e^{-3.33}}{0!}=e^{-3.33}\)
exp(-40/12)## [1] 0.03567399
##or
dpois(0,40/12)## [1] 0.0356739912.2.3 Problem 3
Suppose there are 12 male and 7 female cadets in a classroom. I select 5 completely at random (without replacement).
- Find the probability I select no female cadets.
\(X\): number of female cadets selected out of sample of size 5
\(X\sim \textsf{Hypergeom}(m=7,n=12,k=5)\) and \(\mbox{E}(X)=1.842\) and \(\mbox{Var}(X)=0.905\).
\[ \mbox{P}(\mbox{no female cadets selected})=\mbox{P}(X=0)=\frac{{7\choose 0}{12\choose 5}}{{19\choose 5}} \]
## [1] 0.06811146
##or
dhyper(0,7,12,5)## [1] 0.06811146- Find the probability I select more than 2 female cadets.
Using the same random variable: \[ \mbox{P}(\mbox{more than 2 female})=\mbox{P}(X>2)=1-\mbox{P}(X\leq 2) \]
1-phyper(2,7,12,5)## [1] 0.2365841## [1] 0.2365841