7 Case Study

7.1 Objectives

1. Use R to simulate a probabilistic model.

2. Use basic counting methods.

7.2 Homework

7.2.1 Problem 1

Exactly 2 people with the same birthday - Simulation
Complete a similar analysis for case where exactly 2 people in a room of 23 people have the same birthday. In this exercise you will use a computational simulation.

1. Create a new R Markdown file and create a report. Yes, we know you could use this file but we want you to practice generating your own report.

2. Simulate having 23 people in the class with each day of the year equally likely. Find the cases where exactly 2 people have the same birthday, you will have to alter the code from the Notes more than changing 18 to 23.

(do(10000)*length(unique(sample(days, size = 23, replace = TRUE)))) %>%
  mutate(match = if_else(length == 22, 1, 0)) %>%
  summarise(prob = mean(match))

##     prob
## 1 0.3544

3. Plot the frequency of occurrences as a bar chart.

(do(1000)*length(unique(sample(days, size = 23, replace = TRUE)))) %>%
  gf_bar(~length)

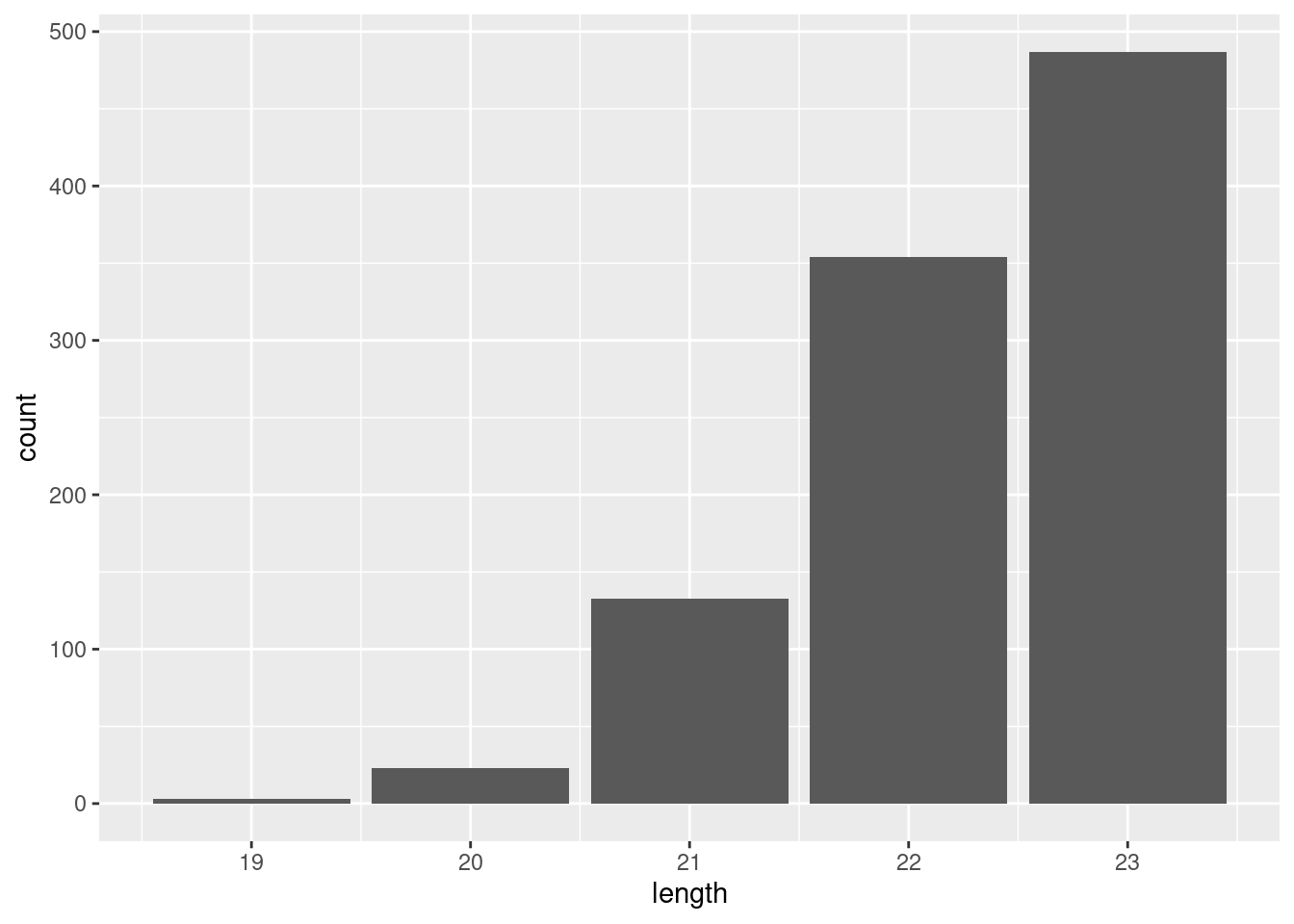
4. Estimate the probability of exactly two people having the same birthday.

In a class of 23 people, there is approximately a 0.36 probability of exactly two people having the same birthday.

7.2.2 Problem 2

Exactly 2 people with the same birthday - Mathematical
Repeat problem 1 but do it mathematically. As a big hint, you will need to use the choose() function. The idea is that with 23 people we need to choose 2 of them to match. We thus need to multiply, the multiplication rule again, by choose(23,2). If you are having trouble, work with a total of 3 people in the room first.

1. Find a formula to determine the probability of exactly 2 people in a room of 23 having the same birthday.

For two people, we have

\[ \binom{23}{2}\times {365 \cdot 364 \cdot 363 \cdot\ ...\ \cdot 344 \over 365^{23}} \]

In R,

choose(23,2)*prod(365:344)/365^23

## [1] 0.3634222

2. Generalize your solution to any number n people in the room and create a function.

In general, we have

\[ \binom{n}{2}\times {365\cdot 364\cdot\ ...\ \cdot (365 - (n - 2))\over 365^{n}} \]

We can write a function in R:

exactly_two <- function(n){
  choose(n,2)*prod(365:(365 - (n - 2))) / 365^n
}

exactly_two(23)

## [1] 0.3634222

3. Vectorize the function.

exactly_two <- Vectorize(exactly_two)

4. Plot the probability of exactly 2 people having the same birthday versus number of people in the room.

gf_line(exactly_two(1:100) ~ seq(1, 100),
        xlab = "Number of People",
        ylab = "Probability of Match",
        title = "Probability of exactly 2 people with matching birthdays")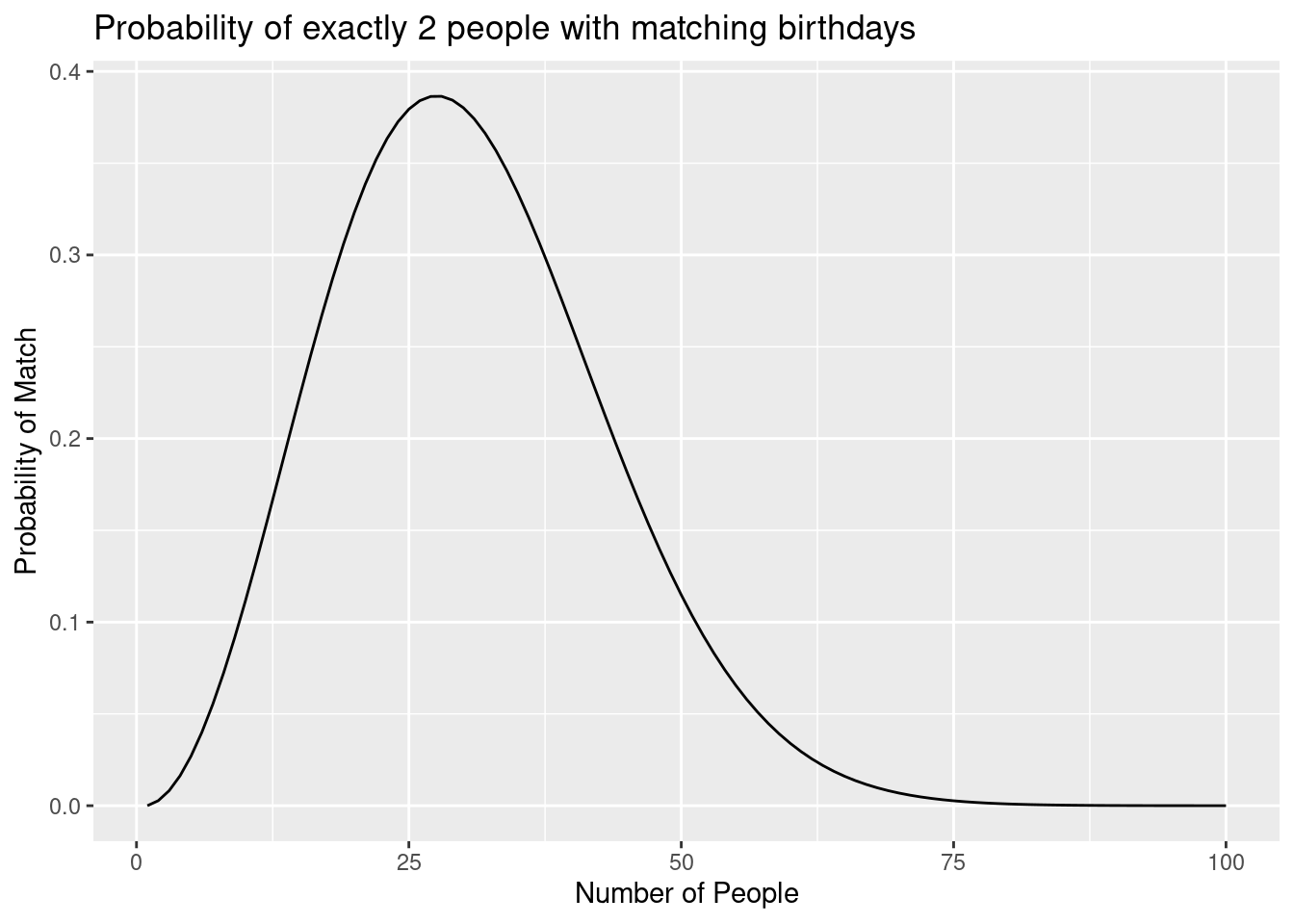

5. Comment on the shape of the curve and explain it.

We want the probability of exactly two people in a room having the same birthday. This is most likely in a room of around 30 people. It’s relatively likely in rooms with between 15-45 people. As the size of the room increases, the probability of exactly two people (and no more) having the same birthday decreases.

6. knit and compile your report.

7.2.2.1 Additional material

By the way, exactly three matches in simulation is hard. We have to table the data

set.seed(10)
temp <- table(sample(days, size = 23, replace = TRUE))
temp

## 
##  13  24  50  72  92 110 137 143 154 155 211 231 263 271 285 330 338 342 344 351 
##   1   1   1   1   1   1   1   1   1   1   1   1   1   1   2   2   1   1   1   1 
## 365 
##   1

(sum(temp == 2) == 2) + 0

## [1] 1

(do(10000)*((sum(table(sample(days, size = 23, replace = TRUE)) == 3) == 1) + 0)) %>%
  summarise(prob = mean(result))

##     prob
## 1 0.0117

Two sets that have same but different birthday

(do(10000)*((sum(table(sample(days, size = 23, replace = TRUE)) == 2) == 2) + 0)) %>%
  summarise(prob=mean(result))

##     prob
## 1 0.1139

(do(10000)*length(unique(sample(days, size = 23, replace = TRUE)))) %>%
  mutate(match = if_else(length == 21, 1, 0)) %>%
  summarise(prob = mean(match))

##     prob
## 1 0.1187

Mathematically exactly 3 is easy. Simulation seems to be off a little or the math formula is off.

choose(23,3)*prod(365:345) / 365^23

## [1] 0.007395218

Textbook